Coefficients binomiaux
Exemple : Cas \(n=3\)
On considère une urne contenant des boules rouges et des boules bleues. On tire au hasard successivement 3 boules que l'on remet à chaque fois dans l'urne. On considère que l'on réussit un tirage lorsque la boule tirée est de couleur rouge.
Ce schéma de Bernoulli peut être représenté par l'arbre suivant :
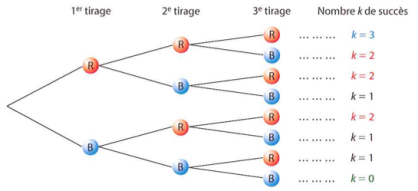
Nous pouvons désormais comptabiliser le nombre de chemins menant à différents nombres de succès :
1 chemin mène à 0 succès
3 chemins mènent à 1 succès
3 chemins mènent à 2 succès
1 chemin mène à 3 succès
Ce que l'on peut noter ainsi :
\(k=0\) | \(k=1\) | \(k=2\) | \(k=3\) |
1 | 3 | 3 | 1 |
Complément :
Ne reconnaissez-vous pas ces 3 nombres ?
Et bien oui ! Ce sont bien des coefficients binomiaux :
\({\Large\binom{3}{0}}\) | \({\Large\binom{3}{1}}\) | \({\Large\binom{3}{2}}\) | \({\Large\binom{3}{3}}\) |
1 | 3 | 3 | 1 |
Complément :
Si on considère qu'un chemin le long des branches de l'arbre sont un n-uplets d'éléments de \(\{S ;\bar S\}\).
Un résultat de \(n\) tirages successifs s'écrit donc \((T_1 ;T_2 ;\cdots ;T_n)\) avec \(T_i\) étant égal à \(S\) ou à \(\bar S\), \(1 \le i \le n\).
Ainsi, le nombre de possibilités d'obtenir \(k\) succès parmi ces \(n\) tirages est égal au nombre de combinaisons de \(k\) éléments parmi les \(n\) éléments, correspondant aux positions des \(k\) \(S\) parmi les \(n\) positions.
Fondamental :
On obtient alors que le nombre de branches menant à \(k\) succès parmi les \(n\) tirages est égal au coefficient binomial \({\Large\binom n k}\).
Remarque : Le chemin de la réussite... ou de l'échec...
De manière générale, sur une répétition de \(n\) (\(n\geq 1\)) épreuves de Bernoulli, il n'y a qu'un seul chemin constitué uniquement de succès, et il n'y a qu'un seul chemin constitué uniquement d'échecs.
On retrouve :
\({\Large{n \choose n}} =1\) et \({\Large{n \choose 0}} =1\)
De même, lorsqu'on a \(n\) épreuves de Bernoulli successives, le nombre de chemin menant à un seul succès (ou un seul échec) est égal à \(n\) puisque ce succès (échec) peut avoir lors du 1er tirage, du 2ème, ... ou du dernier.
On retrouve \({\Large\binom n 1} = n\) et \({\Large\binom n {n-1}}=n\).
Complément :
On retrouvera toutes les propriétés des coefficients binomiaux dans le chapitre de dénombrement.
Complément :
Script pour obtenir le triangle de Pascal.