Application de la convexité
La convexité des fonctions dérivables permet d'établir des inégalités en utilisant les équations des tangentes.
Exemple :
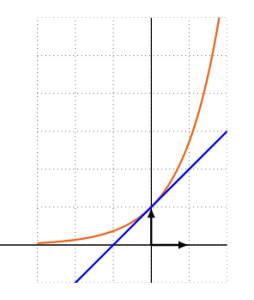
La tangente à la courbe de la fonction exponentielle au point d'abscisse 0 a pour équation \(y=\exp′(0)(x−0)+\exp(0)\), c'est-à-dire \(y=x+1\).
Puisque la fonction exp est convexe sur \(\mathbb R\), la courbe de la fonction exponentielle est donc au-dessus de toutes ses tangentes et donc, en particulier, la tangente au point d'abscisse 0.
On a donc, pour tout réel \(x\), \(e^x\ge x+1\).
On peut retrouver avec cette inégalité, par le théorème de minoration, la limite de la fonction exponentielle en \(+\infty\).