Point d'inflexion
Définition :
Un point d'inflexion est un point où la courbe représentative d'une fonction traverse sa tangente.
Lorsque la courbe représentative d'une fonction admet un point d'inflexion, la fonction change de convexité :
Une fonction convexe devient concave ou inversement en ce point.
\(~\)
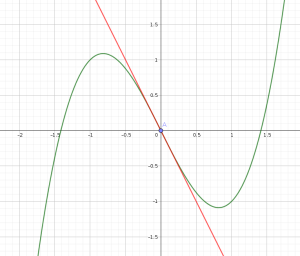
Par exemple, la fonction \(f\) définie par \(f(x)=x^3-2x\) a un point d'inflexion en \(x=0\) : elle est d'abord concave sur \(\mathbb R^-\) et convexe sur \(\mathbb R^+\).
Méthode :
Soit \(f\) une fonction deux fois dérivable sur un intervalle \(I\). La courbe représentative de la fonction \(f\) admet un point d'inflexion au point d'abscisse \(a\) si, et seulement si, \(f\hspace{0.05cm}''\) s'annule en changeant de signe en \(a\).
Attention :
Il ne suffit pas que la dérivée seconde s'annule !
Par exemple, la fonction définie par \(f(x)=x^4\) est convexe, sa dérivée seconde (\(f\hspace{0.05cm}''(x)=12x)\)) s'annule en 0, mais il ne s'agit pas d'un point d'inflexion !
Complément :
On a le même genre de situation avec les extremum locaux d'une fonction :
Si \(f\) admet un extremum local en \(a\), alors \(f′(a)=0\). Cependant, si \(f′(a)=0\), \(f\) admet un extremum local en \(a\) seulement si \(f′\) change de signe en \(a\).
cf la fonction cube dont la dérivée s'annule en 0, alors qu'elle n'a pas d'extremum en \(x=0\).