Exercice : Courbe, sécantes et tangentes
Convexité de la fonction carré sans la dérivée seconde
On va montrer ici que la courbe de la fonction carré est située au dessous de toutes ses cordes.
Pour ceci, on prend deux points \(A\) et \(B\) sur la courbe, de coordonnées \(A(a ;f(a))\) et \(B(b ;f(b))\).
On peut supposer que \(a<b\).
Question
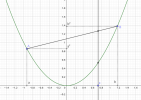
Démontrer que l'équation de la sécante passant par les points \(A(a;a²)\) et \(B(b;b²)\), avec \(a<b\), est :
\(y=(a+b)x-ab\)
Solution
Le coefficient directeur de la droite est donné par \(m=\dfrac{b^2-a^2}{b-a}=a+b\) par la 3ème identité remarquable.
Ainsi, on peut écrire l'équation sous la forme \(y=(a+b)(x-a)+a^2\) car pour \(x=a\), on a bien \(y=a^2\).
En développant, on trouve bien l'équation demandée.
Question
Démontrer que pour tout \(x\) tel que \(a\leq x \leq b\) :
\(x^2\leq (a+b)x-ab\).
Solution
Il suffit donc de démontrer que pour tout \(x\in [a ;b]\), on a \(x^2-(a+b)x+ab\leq 0\) :
On remarque que \(a\) et \(b\) sont les racines de ce polynômes (en les testant ou en calculant \(\Delta\) pour les trouver).
On peut penser aussi aux polynômes de la forme \(x^2-Sx+P\).
Ainsi, le polynôme est du signe contraire du coefficient de \(x^2\), donc négatif, entre les deux racines.
Question
En déduire que la fonction carré est convexe.
Courbe et tangentes
On peut aussi démontrer aisément que la courbe de la fonction carré est au dessus de toutes ses tangentes.
\(~\)
Question
Déterminer pour un \(a\) donné, l'équation de la tangente \(T_a\) en \(a\).
Solution
\(T_a : y=f'(a)(x-a)+f(a)\) donc avec la fonction carré :
\(T_a : y=2ax-a^2\)
Question
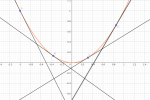
Démontrer que la courbe est au dessus de la tangente \(T_a\).
Solution
Il suffit de prouver que \(\forall x\in\mathbb R, x^2\ge2ax-a^2\), ce qui est équivalent à \(\forall x\in\mathbb R, x^2-2ax+a^2\ge0\).
Or, grâce à la 2ème identité remarquable, on prouve facilement cette inégalité.