Convexité
Définition : Fonction convexe sur un intervalle
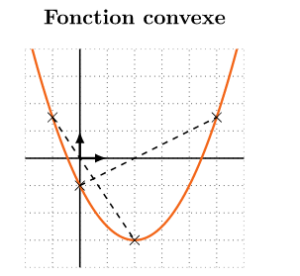
On dit que \(f\) est convexe sur \(I\) lorsque sa courbe représentative est située en‑dessous de chacune de ses sécantes entre les deux points d'intersection.
Définition : Fonction concave sur un intervalle
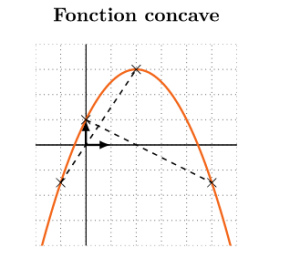
Lorsque la courbe représentative de \(f\) est située au‑dessus de chacune de ses sécantes entre les deux points d’intersection, on dit que \(f\) est concave.
Complément :
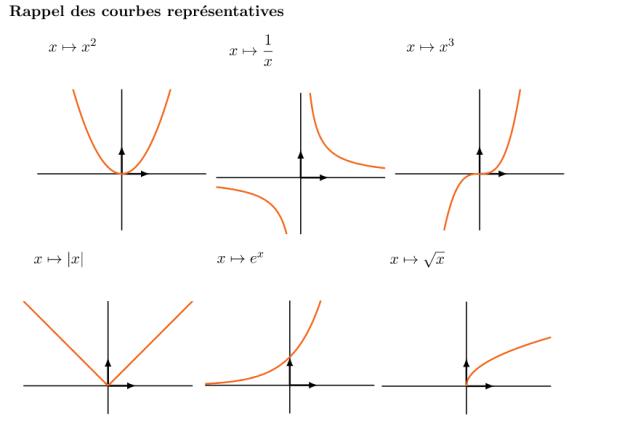
Les fonctions \(x\longmapsto x^2\), \(x\longmapsto |x|\), \(x\longmapsto e^x\) sont convexes sur \(\mathbb{R}\).
La fonction \(x\longmapsto x^3\) est convexe sur \(\mathbb R^+\).
La fonction \(x\longmapsto x^3\) est concave sur \(\mathbb R^-\).
La fonction \(x\longmapsto \sqrt x\) est concave sur \(\mathbb R^+\).
Fondamental :
Dans le cas où la fonction \(f\) est deux fois dérivable, les quatre propositions suivantes sont équivalentes :
\(f\) est convexe sur \(I\).
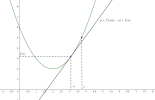
La courbe représentative de \(f\) est entièrement située au‑dessus de ses tangentes, sauf au point de contact.
\(f\hspace{0.05cm}'\) est croissante sur \(I\).
\(f\hspace{0.05cm}''\) est positive sur \(I\).
Complément :
Démonstration :
3. <=> 4. est clair.
1. => 2. nécessite des notions hors programme.
On démontre ici que 4. => 2. , c'est à dire que pour toute fonction dérivable deux fois sur un intervalle \(I\) dont la dérivée seconde est positive, est convexe, donc au dessus de ses tangentes.
En supposant \(f''(x)>0\) sur \(I\), on cherche à prouver que pour tout \(x\in I\), \(f(x)\geq f\hspace{0.05cm}'(a)(x-a)+f(a)\).
Pour ce faire, on va considérer la fonction \(g(x)=f(x)-\left( f\hspace{0.05cm}'(a)(x-a)+f(a)\right)\) sur \(I\).
Cette fonction est une somme de fonction deux fois dérivables, donc elle l'est aussi.
Alors \(g\hspace{0.05cm}'(x)=f\hspace{0.05cm}'(x)-f\hspace{0.05cm}'(a)\).
Étudions le signe de cette dérivée sur \(I\) :
Comme \(f\hspace{0.05cm}''\) est positive, \(f\hspace{0.05cm}'\) est croissante et il en va de même de \(g\hspace{0.05cm}'\).
On peut aussi remarquer que \(g\hspace{0.05cm}''=f\hspace{0.05cm}''\) et comme \(f\hspace{0.05cm}''\geq 0\), \(g\hspace{0.05cm}''\geq 0\) donc \(g\hspace{0.05cm}'\) est croissante.
De plus, \(g\hspace{0.05cm}'(a)=f\hspace{0.05cm}'(a)-f\hspace{0.05cm}'(a)=0\) et \(g(a)=0\).
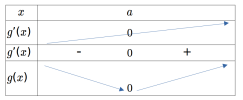
D'où le tableau de variations :
On en déduit donc que la fonction \(g\) est positive sur \(I\) et donc que pour tout \(x\in I\), \(f(x)\geq f\hspace{0.05cm}'(a)(x-a)+f(a)\).
Complément :
Dans le cas où la fonction \(f\) est deux fois dérivable, les quatre propositions suivantes sont équivalentes :
\(f\) est concave sur \(I\).
La courbe représentative de \(f\) est entièrement située au‑dessous de ses tangentes.
\(f\hspace{0.05cm}'\) est décroissante sur \(I\).
\(f\hspace{0.05cm}''\) est négative sur \(I\).