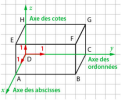
Coordonnées dans l'espace
Nous retrouvons dans l'espace des formules bien connues dans le plan.
On considère dans la suite deux points A et B de coordonnées \((x_A ;y_A ;z_A)\) et \((x_B ;y_B ;z_B)\) dans un repère \((O ;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k})\).
Par exemple, nous pouvons choisir un repère comme celui-ci :
Déterminer les coordonnées de tous les points.
Fondamental : Coordonnées d'un vecteur
Le vecteur \(\overrightarrow{AB}\) a pour coordonnées \(\overrightarrow{AB} \left (\begin{array}{c}x_B-x_A\\y_B-y_A\\z_B-z_A\end{array}\right )\).
Fondamental : Coordonnées du milieu d'un segment
Le milieu du segment \([AB]\) a pour coordonnées\( \left(\dfrac{x_A+x_B}{2} ; \dfrac{y_A+y_B}{2} ; \dfrac{z_A+z_B}{2}\right)\).
Fondamental : Norme d'un vecteur
Si le repère \((O ;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k})\) est orthonormé c'est à dire :
\(\|\overrightarrow{i}\|=\|\overrightarrow{j}\|=\|\overrightarrow{k}\|=1\),
\(\overrightarrow{i}\), \(\overrightarrow{j}\) et \(\overrightarrow{k}\) sont orthogonaux 2 à 2.
Alors \(AB=\|\overrightarrow{AB}\|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}\).
Complément : Avec les coordonnées de vecteurs
Soient \(\overrightarrow{u} \left (\begin{array}{c}x\\y\\z\end{array}\right )\) et \(\overrightarrow{v} \left (\begin{array}{c}x'\\y'\\z'\end{array}\right )\) et \(t\in\mathbb R\).
\(\overrightarrow{u}+\overrightarrow{v} \left (\begin{array}{c}x+x'\\y+y'\\z+z'\end{array}\right )\)
\(t~\overrightarrow{u} \left (\begin{array}{c}tx\\ty\\tz\end{array}\right )\)
\(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires si et seulement si leurs coordonnées sont proportionnelles si et seulement si le tableau suivant est un tableau de proportionnalité :
\(x\)
\(x'\)
\(y\)
\(y'\)
\(z\)
\(z'\)
On cherche donc s'il existe un nombre \(k\) tel que \(x'=k x\), \(y'=k y\), \(z'=k z\).
Si le repère \((O ;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k})\) est orthonormé, on a \(\|\overrightarrow{u}\|=\sqrt{x^2+y^2+z^2}\).
Remarque : Si \(k\in \mathbb R\), alors \(\|\overrightarrow{ku}\|=|k~|\|\overrightarrow{u}\|\) (à démontrer).