Loi binomiale
Définition : Loi binomiale
On appelle Loi binomiale de paramètres \(n\) et \(p\), la loi de probabilité de la variable aléatoire qui associe au schéma de Bernoulli de paramètres \(n\) et \(p\) le nombre \(k\) de succès. La loi binomiale compte donc le nombre de succès lors d'une répétition de \(n\) épreuves de Bernoulli successives, identiques et indépendantes.
Nombre \(k\) de succès | \(0\) | \(1\) | ... | \(n\) |
|---|---|---|---|---|
\(P(X=k)\) | \(P(X=0)\) | \(P(X=1)\) | ... | \(P(X=n)\) |
La Loi binomiale de paramètres \(n\) et \(p\) est notée \(\mathcal{B}(n,p)\).
Exemple : Loi binomiale \(\mathcal B(2 ;p)\)
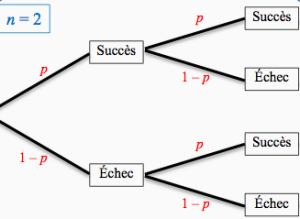
Pour 0 succès, il n'y a qu'un chemin :
\(P(X=0)=(1-p)\times (1-p)=(1-p)^2\).
Pour 1 succès, il y a deux chemins :
\(P(X=1)=(1-p)\times p + p\times (1-p)=2p(1-p)\)
Pour 2 succès, il n'y a qu'un chemin :
\(P(X=2)=p\times p=p^2\)
\(k\) | \(0\) | \(1\) | \(2\) |
|---|---|---|---|
\(P(X=k)\) | \((1-p)^2\) | \(2p(1-p)\) | \(p^2\) |
On peut vérifier que
\(P(X=0)+P(X=1)+P(X=2)=1\)
en développant le membre de gauche.
Exemple : Loi binomiale \(\mathcal B(3 ;p)\)
On considère une urne contenant des boules rouges et des boules bleues. On tire au hasard successivement 3 boules que l'on remet à chaque fois dans l'urne. On considère que l'on réussit un tirage lorsque la boule tirée est de couleur rouge.
Ce schéma de Bernoulli peut être représenté par l'arbre suivant :
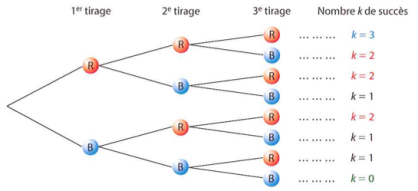
Nous pouvons désormais comptabiliser le nombre de chemins menant à différents nombres de succès :
1 chemin mène à 0 succès
3 chemins mènent à 1 succès
3 chemins mènent à 2 succès
1 chemin mène à 3 succès
Ce que l'on peut noter ainsi :
0 succès | 1 succès | 2 succès | 3 succès |
1 | 3 | 3 | 1 |
Remarque : Le chemin de la réussite...
De manière générale, sur une répétition de \(n\) (\(n\geq 1\)) épreuves de Bernoulli, il n'y a qu'un seul chemin constitué uniquement de succès, et il n'y a qu'un seul chemin constitué uniquement d'échecs.