Exercice : La planche de Galton
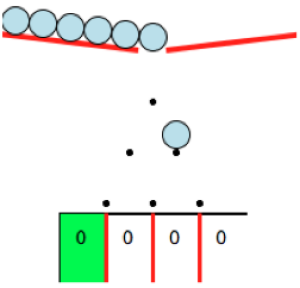
Description du dispositif
On laisse tomber une bille à la verticale du premier clou. Sur chaque clou, on considère qu'une bille à une probabilité \(p\) d'aller sur la droite.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Transcription textuelle
Question
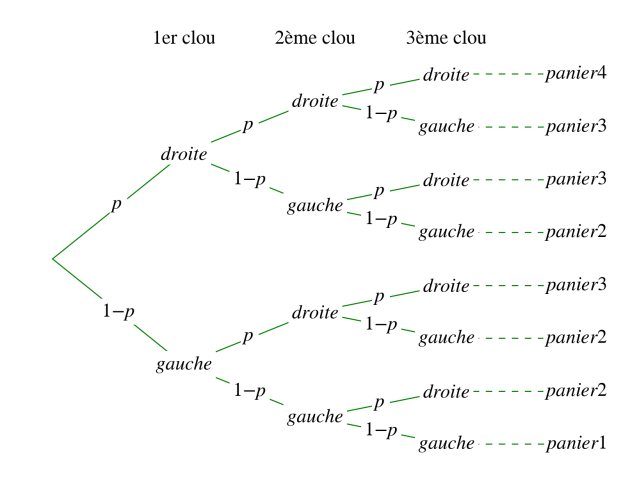
Décrire cette situation à l'aide d'un schéma de Bernoulli.
Question
Quel est, pour chaque panier, le nombre de chemin(s) permettant à une bille d'y tomber ?
Indice
Lier le n° du panier au nombre de fois où la bille tourne à droite.
Solution
Pour les paniers extrêmes, il n'y a qu'un chemin.
Pour le premier panier, il faut que la bille tourne une seule fois à droite. Comme il y a trois rangées, il y a trois possibilités qu'elle tourne à droite une seule fois donc 3 chemins mènent à ce panier. Par symétrie, on en déduit les autres paniers.
N° du panier | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
Nb de chemins | 1 | 3 | 3 | 1 |
Question
Quelle est pour chaque panier la probabilité qu'une bille lancée du sommet de la planche atteigne ce panier.
Indice
Déterminer le nombre total d'issues dans l'expérience aléatoire consistant à répéter trois fois "tourner à gauche ou a droite"
Solution
La planche de Galton est une modélisation concrète d'un schéma de Bernoulli. Il y a 2 issues possibles pour chacune des 3 expériences donc \(2^3=8\) issues au total dans l'univers.
La probabilité pour chacun des paniers est obtenu le nombre de chemins possibles menant à chaque panier par la probabilité obtenu en multipliant les nombres le long des branches.
N° du panier | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
Probabilité | \(1 \times (1-p)^3\) | \(3 \times p^1(1-p)^2\) | \(3 \times p^2 (1-p)^1\) | \(1 \times p^3\) |