Limite finie
Définition :
On dit que la suite \((u_n)\) admet pour limite le réel \(\ell\) si tout intervalle ouvert contenant \(\ell\) contient tous les termes de la suite à partir d'un certain rang.
On dit alors que la suite \((u_n)\) est convergente et converge vers \(\ell\).
On note alors \(\lim\limits_{n \to +\infty} u_n=\ell\).
Complément : Illustration
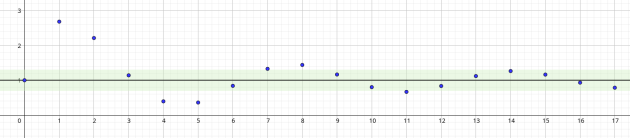
Dans le cas de la suite représentée ci-dessous, on voit que tous les termes à partir du rang 12 appartiennent à un intervalle ouvert contenant 1 (matérialisé par la bande colorée en vert). Et plus l'intervalle ouvert se "resserre" autour de 1, plus il faut aller chercher loin le rang du terme à partir duquel tous les termes de la suite sont dans l'intervalle.
Remarque : Intervalle ouvert
Tout intervalle ouvert contenant \(\ell\) contient un intervalle ouvert centré en \(\ell\) de la forme \(]\ell-\varepsilon ;\ell+\varepsilon[\). On peut donc se contenter de chercher si tout intervalle ouvert de type \(]l-\varepsilon ;l+\varepsilon[\) contient tous les termes de la suite à partir d'un certain rang.
Autrement dit :
\(\forall \varepsilon\in \mathbb{R}, \exists n_0 \in \mathbb{N}\) tel que \(\forall n \geqslant n_0\) , \(u_n\in ]\ell-\varepsilon ;\ell+\varepsilon[\).
Remarque :
\(\lim\limits_{n \to +\infty} u_n=\ell \Longleftrightarrow \lim\limits_{n \to +\infty} u_n - \ell=0\)
Fondamental : Unicité de la limite
Si une suite \((u_n)\) converge vers une limite, alors cette limite est unique.