Épreuve de Bernoulli
Définition : Épreuve de Bernoulli
On appelle épreuve de Bernoulli une expérience aléatoire ayant 2 issues : l'une appelée SUCCÈS est notée \(S\) et l'autre appelée ÉCHEC est notée \(\bar{S}\).
Définition : Loi de Bernoulli
La loi de Bernoulli de paramètre p est la loi de probabilité associée à une épreuve de Bernoulli dont la probabilité de SUCCÈS est \(p\).
La loi de Bernoulli de paramètre \(p\) est donc donnée par le tableau :
Issue | \(S\) | \(\bar{S}\) |
|---|---|---|
Probabilité | \(p\) | \(1-p\) |
Complément : Arbre associé à une épreuve de Bernoulli
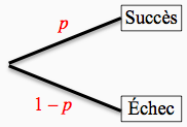
Si la probabilité d'obtenir un succès est égale à \(p\) alors la probabilité d'un échec est égale à \(1 – p\) .
Exemple : Lancer d'un dé
On lance un dé à 6 faces. On considère un SUCCÈS lorsque le dé tombe sur 1 ou 6.
L'univers Ω associé à cette expérience est {1,2,3,4,5,6}.
L'événement SUCCÈS est \(S=\{1,6\}\).
L'événement ÉCHEC est \(\bar{S}=\{2,3,4,5\}\).
\(P(S)=\dfrac{1}{3}\)
\(P(\bar{S})=\dfrac{2}{3}\)
On a défini une épreuve de Bernoulli de paramètre \(\dfrac{1}{3}\).