Exercice : Dépasser un seuil
Une somme de 10 000 euros est placée à un taux annuel de 3,5%. On note \(u_n\) le capital au bout de \(n\) années. Au bout de combien d'années ce capital double-t-il ?
Il y a plusieurs méthodes pour répondre à cette question. Nous allons en voir deux qui utilisent la calculatrice mais de manières différentes.
Question
Donner une formule de récurrence permettant de calculer la suite \((u_n)\).
Solution
On peut choisir d'exprimer les termes de la suite \(u_n\) en milliers d'euros (mais ce n'est pas une obligation).
\(u_0=10\)
\(u_{n+1}=u_n\times 1,035\)
Question
A l'aide de la fonction suites de la calculatrice, dresser un tableau de valeur de la suite \(u_n\) et en déduire la réponse à la question posée.
Solution
Méthode : Tabuler une suite définie par récurrence sur Numworks
Dans l'appli Suites :
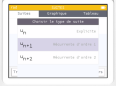
On accède ensuite au terme \(u_n\) en utilisant la boîte à outils.
Méthode : Tabuler une suite définie par récurrence sur Casio
Sélectionner Menu Recur(8) puis sélectionner an+1 : ![]()
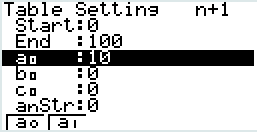
Dans SET dur la touche \(\fbox{F5}\), définir le nombre de termes calculés et le terme initial de la suite : a0=10
De retour sur l'écran Recursion, appuyer sur \(\fbox{n.an}\) (\(\fbox{F4}\)) pour saisir la formule de récurrence exprimant \(a_{n+1}\) en fonction de \(a_n\).
Vous ferez appel à \(a_n\) au moyen de la touche \(\fbox{F2}\).
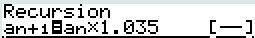
Les valeurs de la suite s'obtiennent par la fonction TABL (touche \(\fbox{F6}\)).
On lit ainsi sur l'écran la valeur de \(u_{20}=19,9\) et \(u_{21}=20,5\)
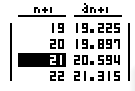
Le capital a donc doublé au bout de 21 ans.
Méthode : Tabuler une suite définie par récurrence sur TI
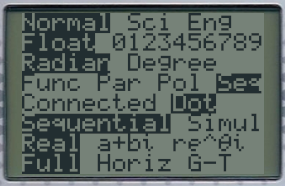
Choisir mode puis positionnez le mode suite (Seq)
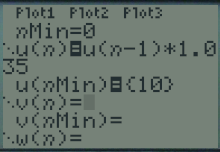
Par la touche f(x), entrer la formule de récurrence donnant le terme \(u_n\) en fonction de \(u_{n-1}\).
L'expression \(u_{n-1}\) s'obtient par \(\fbox{2nde}\ \fbox{7}\ \fbox{(}\ \fbox{x,t,o,n}\ \fbox{-}\ \fbox{1}\ \fbox{)}\)
Renseignez la valeur de \(u_0\) dans u(nMin) et 0 dans nMin.
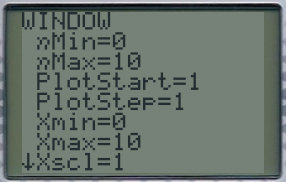
Définir dans fenêtre les valeurs min et max pour n.
Les valeurs de la suite s'obtiennent par la fonction \(\fbox{2nde}\ \fbox{graphe}\).
On lit ainsi sur l'écran la valeur de \(u_{20}=19,9\) et \(u_{21}=20,5\).
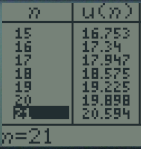
Le capital a donc doublé au bout de 21 ans.
Question
On considère l'algorithme suivant :
Initialisation :
... n prend la valeur 0
... u prend la valeur 10
Traitement :
... Tant que u < 20 Faire
... ... n prend la valeur n+1
... ... u prend la valeur u * 1.035
... Fin Tant que
Sortie :
... Afficher n
Compléter le tableau suivant :
Etape 0 | Etape 1 | Etape 2 | |
|---|---|---|---|
variable \(n\) | 0 | ||
variable \(u\) | 10 | ||
Condition \(u<20\) |
A quoi sert cet algorithme ?
Quel est le rôle de chacune des variables ?
Expliquer son fonctionnement.
Solution
Etape 0 | Etape 1 | Etape 2 | |
|---|---|---|---|
variable \(n\) | 0 |
|
|
variable \(u\) | 10 |
|
|
Condition \(u<20\) |
|
|
|
On voit donc dans l'exécution pas à pas de l'algorithme que la variable \(n\) permet de comptabiliser le nombre d'années et que \(u\) contient la valeur de \(u_n\).
Tant que le capital n'a pas doublé, on continue à augmenter de dernier de 3,5%
Dès qu'il a doublé, on sort de la boucle et on affiche le nombre d'années nécessaires au doublement du capital.
Question
Programmer cet algorithme et répondre à la question posée initialement.
Indice
On pourra le programmer sur Python sur sa calculatrice ou sur ordinateur.
Solution
Méthode : A l'aide du langage python
Le programme suivant implémente l'algorithme en utilisant le langage Python. On peut l'exécuter pas à pas.
La valeur retournée est 21, ce qui répond à la question initialement posée : Le capital a donc doublé au bout de 21 ans.