Exercice : Extrait d'un exercice du baccalauréat italien 

Observer la figure suivant :

Question

La courbe rouge représente la fonction sinus.

On cherche à déterminer l'aire de la partie coloriée.

Indice

Indices :

\(\sin'=\cos\) et \(\cos ' = -\sin\).

Solution

Répondre aux questions suivantes.

Question

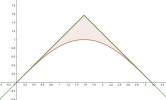
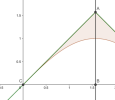
Déterminer l'équation des droites portant les deux segments.

Question

Déterminer l'abscisse des point \(A\) et \(B\).

Question

En déduire l'aire du triangle ABC :

Question

Déterminer l'aire sous la courbe de la fonction sin sur l'intervalle \([0 ;\dfrac \pi 2]\).

Question

Déterminer l'aire demandée.

Solution

L'aire cherchée vaut \(\dfrac {\pi^2}{4}-2\approx 0,4673\).

Question

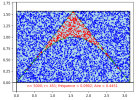
Afin de vérifier nos calculs, nous allons utiliser la méthode de Monte-Carlo.

Écrire un programme python qui génère des points dans le rectangle de base \([0 ;\pi]\) et de hauteur \([0 ;1]\) et déterminant la proportion de point à l'intérieur du domaine précédent par rapport au rectangle.

Solution

Par la loi des grands nombres, la fréquence de points à l'intérieur du domaine par rapport au rectangle est proche de la probabilité d'obtenir un point dans le domaine quand le nombre de points est grand.

Or, la probabilité est égale à \(\dfrac{\text{aire du domaine}}{\text{aire du rectangle}}\).

Ainsi, on approxime l'aire en calculant la fréquence multipliée par l'aire du rectangle \(\dfrac{\pi^2}2\) :

Script

script_montecarlo.py [py, 1,2 ko]