La loi binomiale

\(X\) suit la loi binomiale de paramètre \(n=6\) et \(p=\dfrac 1 2\).

\(P(X=0)=\binom 6 0 \left( \frac 1 2\right)^0\left( \frac 1 2\right)^6=1\times 1\times \frac 1 {64}=\frac 1 {64}=0,015625\).

\(P(X=1)=\binom 6 1 \left(\frac 1 2\right)^1 \left(\frac 1 2\right)^5=6\times \left(\frac 1 2\right)^6=6\times \frac 1 {64}=\frac 6 {64}=0,09375\).

\(P(X\le 1)=P(X=0)+P(X=1)\approx0,109375\) d'après ce qui précède.

Pour la valeur exacte, on obtient \(\dfrac1{2^6}+\binom61\times\dfrac1{2^1}\dfrac1{2^5}=\dfrac7{64}\).

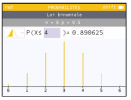
Pour \(P(X\le 4)\), on peut utiliser la version cumulée de la loi binomiale sur la calculatrice et on trouve 0,890625  environ:

On peut aussi faire le calcul manuellement en écrivant que \(P(X\le 4)=1-P(X\ge5)=1-P(X=5)-P(X=6)=1-\dfrac7{64}=\dfrac{57}{64}\).

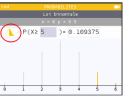
Sur la numworks, on choisit l'application Probabilité, Binomiale, \(n=6\) et \(p=1/2\), puis on obtient ceci :

Attention à bien choisir la version cumulée à gauche (ce qui est entouré en rouge).

On peut aussi faire le calcul manuellement en écrivant que \(P(X\ge 5)=P(X=5)+P(X=6)=\dfrac6{64}+\dfrac1{64}=\dfrac7{64}\).