Exercice : Table de la loi binomiale
\(X\) est une variable aléatoire qui suit la loi binomiale de paramètres \(n=5\) et \(p=0,7\).
Question
Afficher avec la calculatrice la loi de probabilité de \(X\).
Solution
La loi de probabilité de \(X\) est de tableau donnant :
en première liste, le nombre de succès possible, donc tous les entiers \(k\) allant de \(0\) à \(n\),
en deuxième liste, les probabilités d'obtenir exactement 0, 1, ..., \(n\) succès parmi les \(n\) épreuves.
A l'aide de la numworks
On va utiliser l'application suite de la calculatrice :
On définit une suite explicite, on clique sur la boîte à outils et on choisit "Probabilité" :
On choisit alors Loi binomiale et binompdf(m,n,p) :
On prend pour valeur de \(m\) l'indice \(n\), pour \(n\), et \(p\) on prend les valeurs de souhaitées :
exemple : pour obtenir la table des valeurs de la lo binomiale de paramètres \(n=12\), et \(p=0,2\), on met :
\(~\)
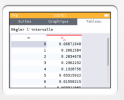
On peut alors obtenir la table de la loi :
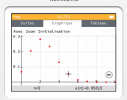
ou la représentation graphique :
A l'aide de TI
Tout d'abord, on crée dans la liste L1 les valeurs de k possibles au moyen de la fonction SEQ se trouvant dans \(\fbox{2nd}~ \fbox{LIST} ~ \fbox {OPS}~ ~ 5 :seq\). La fonction s'utilise avec la syntaxe ci-contre :

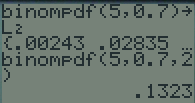
Ensuite on calcule la loi de probabilité de la loi binomiale de paramètres n=5 et p=0,7 au moyen de la fonction binompdf se trouvant dans \(\fbox{2nd}~\fbox{DISTR}~ ~0 :binompdf(\).
La fonction s'utilise avec la syntaxe ci-contre.
La première commande permet de stocker toute la loi de probabilité dans la liste L2.
La seconde commande permet d'obtenir la probabilité \(\mathbb P(X=2)\).
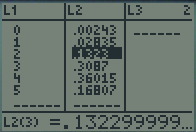
La loi de probabilité se trouve alors disponible dans le menu \(\fbox{STAT}~ ~1 : Edit...\).
Complément : Utilisation de la fonction TABLE des fonctions
Une autre méthode est possible : utiliser la fonction TABLE de VALEURS de la calculatrice avec la fonction \(Y1=Binompdf(5,0.7,X)\).
Cette méthode, applicable uniquement sur TI, est décrite dans le document papier du paragraphe suivant.
\(~\)
A l'aide de Casio

Tout d'abord on crée dans la liste L1 les valeurs de k possibles au moyen de la fonction SEQ se trouvant dans \(\fbox{OPTN}~ \fbox{F1}~LIST ~ \fbox {F5}~Seq\). La fonction s'utilise avec la syntaxe ci-contre.
Ensuite on calcule la loi de probabilité de la loi binomiale de paramètres n=5 et p=0,7 en allant dans le \(\fbox{MENU}~ STAT 2\). On retrouve la Liste 1 remplie avec les valeurs de 0 à 5. On met \(\fbox{List 2}\) en surbrillance puis \(\fbox{F5}~ DIST~ ~ \fbox{F5} ~ BINM~ ~ \fbox{F1}~Bpd\). On remplit ensuite les paramètres comme indiqué ci-contre.:


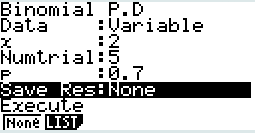
Le paramétrage suivant de la fenêtre Bpd permet de calculer \(\mathbb P(X=2)\) pour X suivant la loi Binomiale de paramètres \(n=5\) et \(p=0,7\).