Exercice : Première méthode pour calculer une intégrale dans le cas d'une fonction affine

Nous allons calculer notre première intégrale pour une fonction simple : une fonction affine.

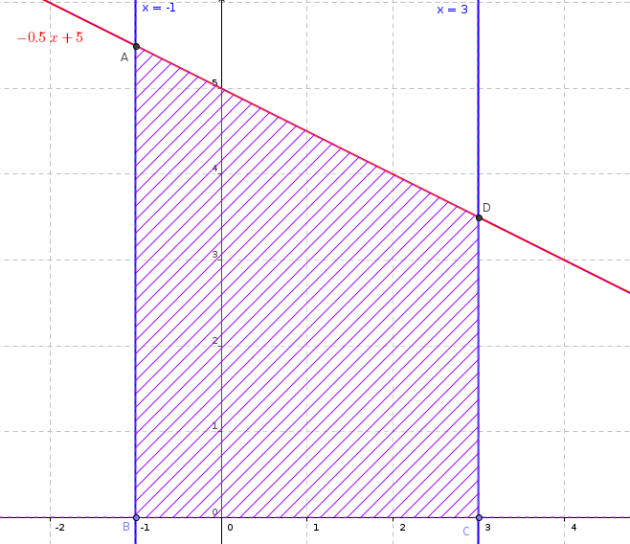
On définit \(f :x\longmapsto -\dfrac{1}{2}x+5\) et on note \(\mathcal Cf\) sa courbe représentative.

Question

Hachurer sur un graphique l'aire représentée par \(\displaystyle\int_{-1}^3 -\dfrac{1}{2}x+5~\mathrm dx.\)

Indice

Il faut dessiner la droite d'équation \(y=-\dfrac{1}{2}x+5\) mais aussi \(x=-1\) et \(x=3.\)

Solution

Question

Calculer \(\displaystyle\int_{-1}^3 -\dfrac{1}{2}x+5~\mathrm dx.\)

Indice

On pourra utiliser le graphique réalisé et les connaissances de géométrie de base.

Indice

L'aire d'un trapèze est \(\dfrac{(Petite~base+Grande~base)\times Hauteur}{2}\).

Solution

Avec les notations de la figure, \(\mathcal{A}=\dfrac{(CD+AB)\times BC}{2}\) donc :

\(\mathcal{A}=\dfrac{(3,5+5,5)\times 4}{2}\) donc \(\mathcal{A}=18\) unités d'aire,

donc \(\displaystyle \int_{-1}^3 -\dfrac{1}{2}x+5~\mathrm dx=18.\)