Théorème des valeurs intermédiaires
Fondamental : Théorème des valeurs intermédiaires (TVI). Propriété admise.
Soit \(f\) une fonction définie et continue sur un intervalle \(I\). Soient \(a\) et \(b\) deux réels appartenant à cet intervalle. On peut supposer \(a<b\).
Alors, pour tout réel \(k\) compris entre \(f(a)\) et \(f(b)\), il existe au moins un réel \(c\) compris entre \(a\) et \(b\) tel que \(f(c)=k\).
Autrement dit, l'équation \(f(x)=k\) admet au moins une solution \(c\) comprise entre \(a\) et \(b\).
Remarque : dans ce théorème, si \(f(a) \)est supérieur à \(f(b)\), la propriété s'écrit :
Pour tout réel \(k\) compris entre \(f(b)\) et \(f(a)\), il existe au moins un réel \(c\) compris entre \(a\) et \(b\) tel que \(f(c)=k\).
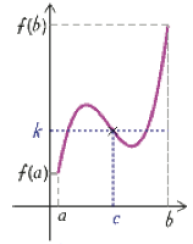
f n'est pas strictement monotone
Complément : Cas où \(f\) est monotone
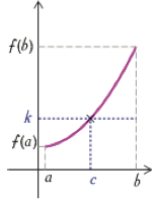
La fonction f est strictement monotone
Si, de plus, la fonction \(f\) est strictement monotone sur l'intervalle I, alors le réel \(c\) est unique.
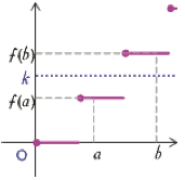
Attention : La continuité est une hypothèse essentielle du théorème
Si la fonction \(f\) n'est pas continue, il est possible que pour un réel \(k\) compris entre \(f(a)\) et \(f(b)\), il n'existe aucune solution à l'équation \(f(x)=k\) ! !