Exercice : Solution approchée d'une équation
On considère la fonction \(f(x)=x^3+x\).
On cherche à déterminer la ou les solutions éventuelles de l'équation \(f(x)=5\).
Il existe des formules très complexes pour déterminer la ou les valeurs exactes des solutions (les formules de Cardan) mais elles ne sont pas au programme de terminale car trop difficiles à mettre en œuvre.
Question
Montrer que la fonction \(f\) est continue et strictement monotone sur l'intervalle \(I=[1 ;2]\).
Solution
La fonction \(f\) est une fonction usuelle (polynôme) sans problème particulier. Elle est donc définie et continue sur \(\mathbb{R}\).
Pour déterminer ses variations, on s'intéresse au signe de sa dérivée : \(f'(x)=3x^2+1\).
Un carré étant toujours positif, la dérivée \(f'\) est toujours strictement positive et la fonction \(f\) est donc strictement croissante sur \(\mathbb{R}\).
Question
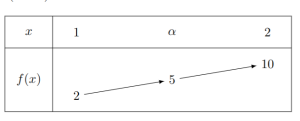
Montrer que l'équation \(f(x)=5\) admet une solution unique sur \(I\).
Solution
La fonction \(f\) est continue,
La fonction \(f\) est strictement croissante sur \([1 ;2]\),
\(f(1)=2\) et \(f(2)=8+2=10\) donc \(f(1)<5<f(2)\).
Cela nous permet d'établir le tableau de variations ci-contre.
Le théorème des valeurs intermédiaires permet donc d'affirmer qu'il existe une unique solution \(\alpha\in [1 ;2]\) tel que \(f(c)=5\).
Question
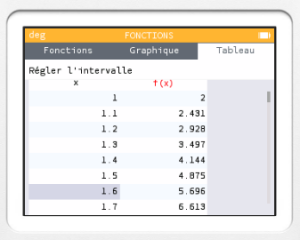
A l'aide de la calculatrice, déterminer une valeur approchée de la solution de l'équation \(f(x)=5\) à 0,1 près.
Indice
On pourra utiliser la fonction tableau de valeurs.
Solution
L'écran ci-contre reproduit le tableau de valeurs affiché par la calculatrice entre 1 et 2 avec un pas de 0,1
On y voit clairement apparaître que la solution \(c\) cherchée est comprise entre 1,5 et 1,6 puisque \(f(1,5)<5<f(1,6)\).
Complément : Plus de précision ?
Si on cherche une valeur approchée plus précise de la solution, on utilisera à nouveau la fonction table entre \(1,5\) et \(1,6\) avec un pas de \(0,01\) et ainsi de suite.