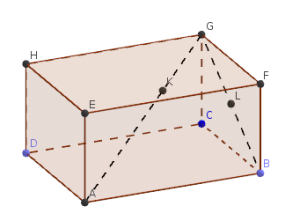
Exercice : Démontrer l'alignement ou l'appartenance à un plan
On considère :
un pavé droit \(ABCDEFGH\),
Les points \(K\) et \(L\) définis par \(\overrightarrow{AK}=\dfrac{2}{3}\overrightarrow{AG}\) et \(\overrightarrow{AL}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AH}\)
Question
En exprimant \(\overrightarrow{HK}\) et \(\overrightarrow{HL}\) en fonction de \(\overrightarrow{AB}\) et \(\overrightarrow{AH}\), démontrer que les points \(H\), \(K\) et \(L\) sont alignés.
Solution
\(\overrightarrow{HK}=\overrightarrow{HA}+\overrightarrow{AK}=-\overrightarrow{AH}+\dfrac{2}{3}(\overrightarrow{AB}+\overrightarrow{BG})\)
Or\( \overrightarrow{BG}=\overrightarrow{AH}\).
Donc \(\overrightarrow{HK}=-\overrightarrow{AH}+\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AH}\).
D'où \(\overrightarrow{HK}=\dfrac{2}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AH}\).
D'autre part, \(\overrightarrow{HL}=\overrightarrow{HG}+\overrightarrow{GL}\).
Or \(\overrightarrow{HG}=\overrightarrow{AB}\) et \(\overrightarrow{GL}=-\dfrac{1}{2}\overrightarrow{AH}\) par construction.
Donc \(\overrightarrow{HL}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AH}\).
On constate donc que \(\overrightarrow{HK}=\dfrac{2}{3}\overrightarrow{HL}\) ce qui démontre que les points \(H\), \(K\) et \(L\) sont alignés.
Simulation :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Question
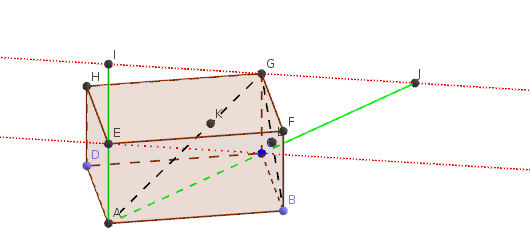
Soit \(I\) le symétrique de \(A\) par rapport à \(E\) et \(J\) le symétrique de \(A\) par rapport à \(C\).
Démontrer que les droites \((EC)\) et \((GI)\) sont parallèles.
Solution
On sait par construction que \(\overrightarrow{EI}=\overrightarrow{AE}=\overrightarrow{CG}\) donc \(EIGC\) est un parallélogramme donc \(\overrightarrow{CE}=\overrightarrow{GI}\) ce qui prouve le parallélisme des deux droites.
Question
Justifier que \(\overrightarrow{AG}=\dfrac{1}{2}\overrightarrow{AI}+\dfrac{1}{2}\overrightarrow{AJ}\).
Solution
\(\overrightarrow{AG}=\overrightarrow{AE}+\overrightarrow{EG}=\overrightarrow{AE}+\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{AI}+\dfrac{1}{2}\overrightarrow{AJ}\)
Question
Le point \(K\) appartient-il au plan \((AIJ)\) ?
Quelles sont ses coordonnées dans le repère \((A,I,J)\) ?
Solution
\(\overrightarrow{AK}=\dfrac{2}{3}\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AI}+\dfrac{1}{3}\overrightarrow{AJ}\) d'après la question précédente.
\(K\) peut donc se décomposer selon les vecteurs \(\overrightarrow{AI}~ \text{et} ~\overrightarrow{AJ}\) du plan \((AIJ)\), ce qui montre que \(K\) appartient au plan \((AIJ)\).
Ses coordonnées dans le repère \((A,I,J)\) sont \(\left(\dfrac{1}{3} ;\dfrac{1}{3}\right)\).