Produit scalaire dans le plan

Produit scalaire dans le plan

 
♦ Les différentes façons de calculer un produit scalaire: Cours de math en vidéo
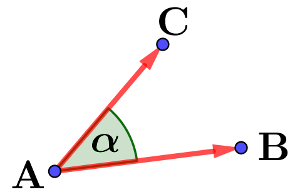
  • Avec un angle
    $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm AC}=\rm AB\times AC\times \cos \widehat{BAC}=\rm AB\times AC\times \cos \alpha$
    $\rm \widehat{BAC}$ est ce qu'on appelle un angle géométrique.
    Sa mesure est toujours comprise entre 0 et 180°
    ou en radian entre 0 et $\pi$ rad.
    Penser à utiliser cette formule quand on connait
    un angle et les 2 longueurs adjacentes.


  • Avec des vecteurs colinéaires
    • Si les vecteurs sont colinéaires et de même sens:
    $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm AC}=\rm AB\times AC$
    C'est un cas particulier de la formule:
    $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm AC}=\rm AB\times AC\times \cos \widehat{BAC}$
    lorsque $\rm \widehat{BAC}=0$ et donc $\rm \cos\widehat{BAC}=1$


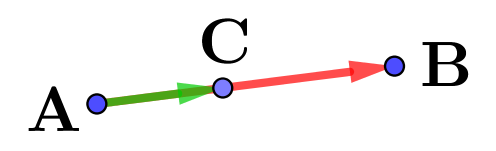
    • Si les vecteurs sont colinéaires et de sens opposé:
    $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm AC}=-\rm AB\times AC$
    C'est un cas particulier de la formule:
    $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm AC}=\rm AB\times AC\times \cos \widehat{BAC}$
    lorsque $\rm \widehat{BAC}=\pi$ rad et donc $\rm \cos\widehat{BAC}=-1$


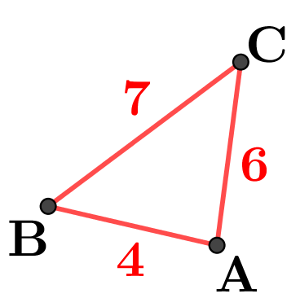
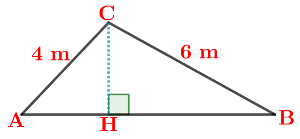
  • Avec les longueurs
    $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm AC}=\rm \dfrac12(AB^2+AC^2-BC^2)$
    Penser à utiliser cette formule,
    quand on connait les 3 longueurs dans un triangle.


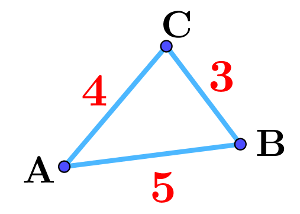
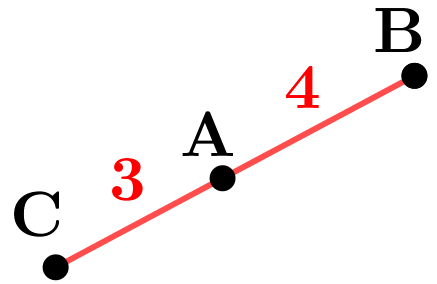
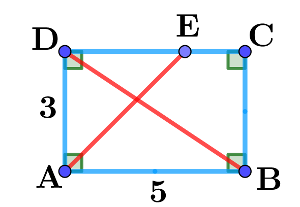
    Dans cet exemple:
    $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm AC}=\rm \dfrac12(5^2+4^2-3^2)=16$

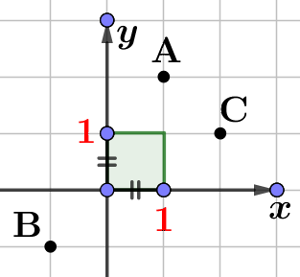
  • Avec les coordonnées
    $\overrightarrow{u}\cdot \overrightarrow{v}=xx'+yy'$
    avec $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$


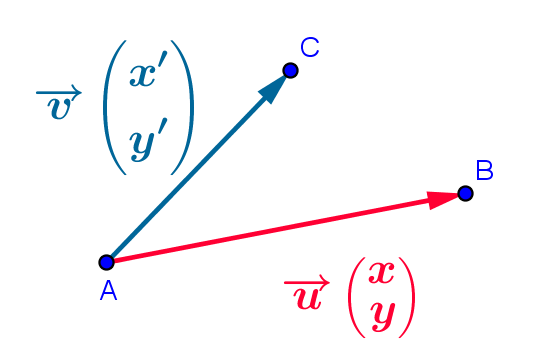
    Pour calculer le produit scalaire avec les coordonnées,
    il faut être dans un repère orthonormé !

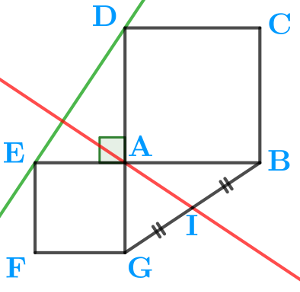
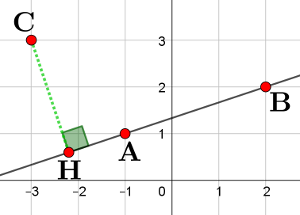
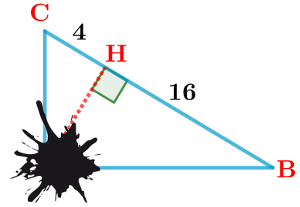
  • Avec la projection orthogonale
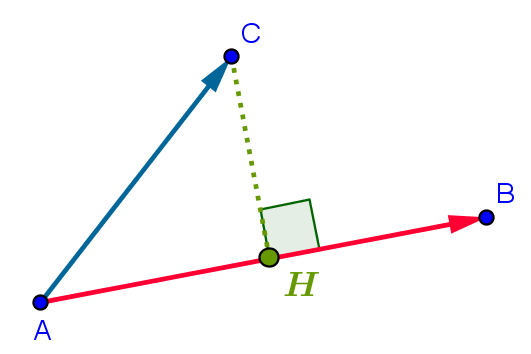
    $\rm \overrightarrow{AB}\cdot \overrightarrow{AC}=\overrightarrow{AB}\cdot \overrightarrow{AH}$
    Et comme $\rm \overrightarrow{AB}$ et $\rm \overrightarrow{AH}$ sont colinéaires,
    on se ramène à un calcul de produit scalaire
    avec des vecteurs colinéaires, ce qui est plus simple.


    $\rm \overrightarrow{AB}\cdot \overrightarrow{AC}=\overrightarrow{AC}\cdot \overrightarrow{AK}$
    Et comme $\rm \overrightarrow{AC}$ et $\rm \overrightarrow{AK}$ sont colinéaires,
    on se ramène à un calcul de produit scalaire
    avec des vecteurs colinéaires, ce qui est plus simple.


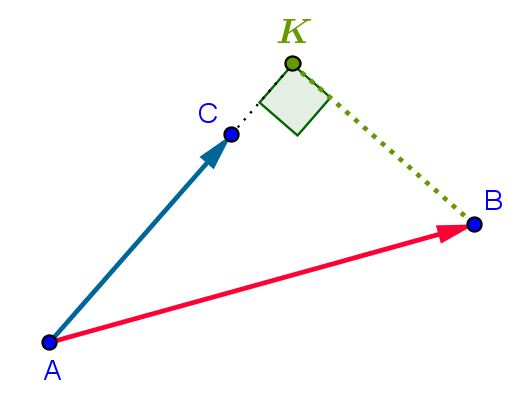
    On peut projeter,
    soit le premier vecteur sur le deuxième
    soit le deuxième vecteur sur le premier

    Donc ne pas oublier qu'il y a deux possibilités !

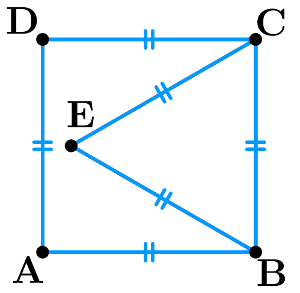
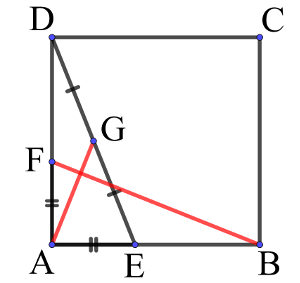
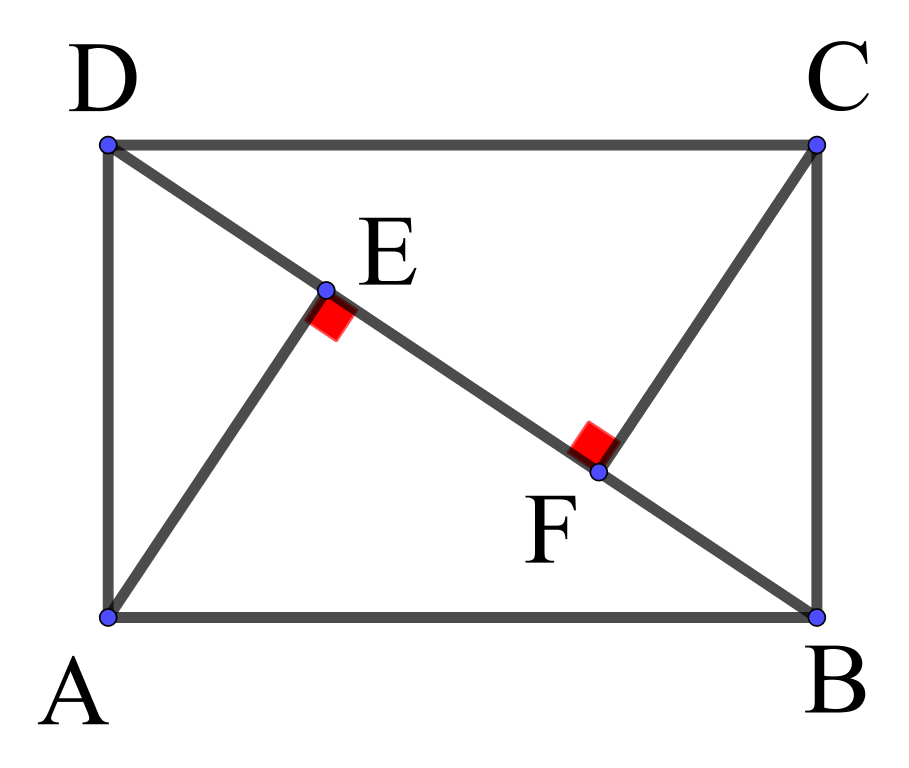
  • Avec une décomposition
    Penser à décomposer les vecteurs,
    en utilisant les angles droits
    ou les sommets de la figure.
    Puis développer!

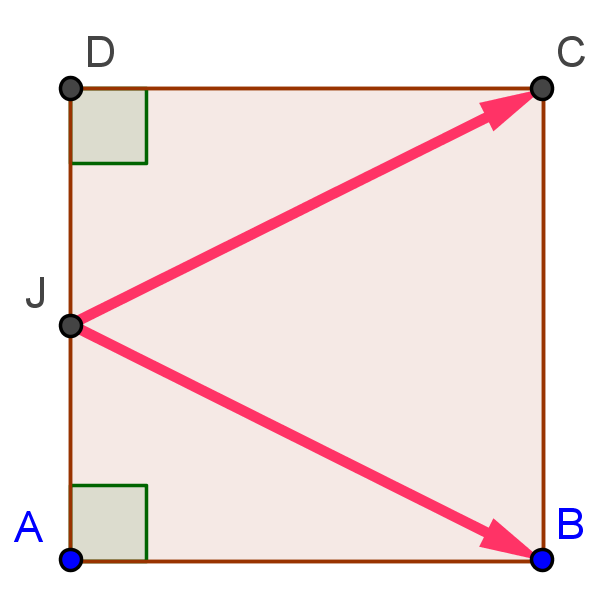
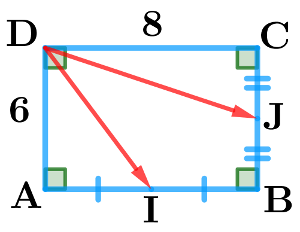
    $\rm \overrightarrow{JB}\cdot \overrightarrow{JC}=(\overrightarrow{JA}+\overrightarrow{AB})\cdot(\overrightarrow{JD}+\overrightarrow{DC})$

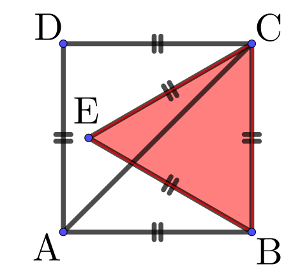
  • Conseils
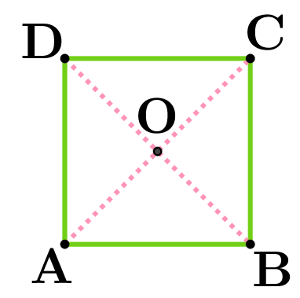
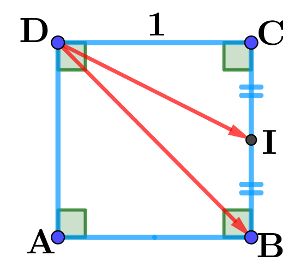
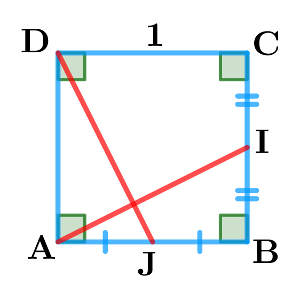
    Quand il y a un rectangle, un carré,
    penser à introduire un repère orthonormé!
    • Puis trouver les coordonnées des points qui vous intéressent.
    • Puis calculer les coordonnées des vecteurs.
    • Puis calculer le produit scalaire avec les coordonnées.




Corrigé en vidéo
Exercices 1:

Calculer un produit scalaire avec les projetés orthogonaux


$\rm ABCD$ est un carré de centre $\rm O$ et côté $2$.
Calculer les produits scalaires suivants:
      $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm CD}$
      $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm BD}$
      $\overrightarrow{\rm CB}\cdot \overrightarrow{\rm AO}$
      $\overrightarrow{\rm OA}\cdot \overrightarrow{\rm OB}$		      
Corrigé en vidéo
Exercices 2:

Calculer un produit scalaire avec la formule du cosinus


$\rm ABCD$ est un carré de côté $4$.
Calculer les produits scalaires suivants:
      $\overrightarrow{\rm CE}\cdot \overrightarrow{\rm CB}$
      $\overrightarrow{\rm EB}\cdot \overrightarrow{\rm EC}$
      $\overrightarrow{\rm CD}\cdot \overrightarrow{\rm EC}$
      $\overrightarrow{\rm CD}\cdot \overrightarrow{\rm CA}$		      
Corrigé en vidéo
Exercices 3:

Calculer un produit scalaire avec avec la formule du cosinus


$\rm ABCD$ est un losange de côté $2$ et $\rm BD=2$.
Calculer les produits scalaires suivants:
      $\overrightarrow{\rm DB}\cdot \overrightarrow{\rm CA}$       $\overrightarrow{\rm CD}\cdot \overrightarrow{\rm AB}$
      $\overrightarrow{\rm CA}\cdot \overrightarrow{\rm DC}$       $\overrightarrow{\rm BD}\cdot \overrightarrow{\rm DA}$
      $\overrightarrow{\rm BD}\cdot \overrightarrow{\rm DB}$       $\overrightarrow{\rm DC}\cdot \overrightarrow{\rm AD}$		      
Corrigé en vidéo
Exercices 4:

Les 6 techniques pour calculer un produit scalaires


()
Dans chaque cas, calculer le produit scalaire $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm AC}$:
Corrigé en vidéo
Exercices 5:

Maîtriser les formules pour calculer un produit scalaire et des normes


Dans un repère orthonormé, on considère deux vecteurs $\vec u$ et $\vec v$ tels que:
$||\vec u||=2$ et $||\vec v||=5$ et $(\vec u ;\vec v)=\dfrac{5\pi}6$.
Calculer: $\vec u\cdot \vec v$        $(\vec v-\vec u)(\vec u+3\vec v)$        $||\vec u+\vec v||$        $||\vec u-2\vec v||$.
Corrigé en vidéo
Exercices 6:

Calculer un produit scalaire de deux façons différentes


$\rm ABCD$ est un rectangle. $\rm AD=6$ et $\rm DC=8$.
$\rm I$ est le milieu de $\rm [AB]$ et $\rm J$ celui de $\rm [BC]$.
1. A l'aide d'un repère bien choisi, calculer $\overrightarrow{\rm DI}\cdot \overrightarrow{\rm DJ}$.
2. Sans utiliser de coordonnées, calculer $\overrightarrow{\rm DI}\cdot \overrightarrow{\rm DJ}$. 		   
Corrigé en vidéo
Exercices 7:

Calculer un angle à l'aide d'un produit scalaire


$\rm ABCD$ est un carré de côté $1$.
$\rm I$ est le milieu de $\rm [BC]$.
En calculant de deux manières $\overrightarrow{\rm DI}\cdot \overrightarrow{\rm DB}$,
déterminer la mesure de l'angle $\widehat{\rm BDI}$ à 0,1 degré près. 		   
Corrigé en vidéo
Exercices 8:

Utiliser un produit scalaire pour montrer que des droites sont perpendiculaires


$\rm ABCD$ est un carré de côté $1$.
$\rm I$ est le milieu de $\rm [BC]$ et $\rm J$ celui de $\rm [AB]$.
Démontrer que $\rm (AI)$ et $\rm (DJ)$ sont perpendiculaires:
a) à l'aide d'un repère.
b) sans utiliser de repère. 		   
Corrigé en vidéo
Exercices 9:

Utiliser un produit scalaire pour montrer que des droites sont perpendiculaires


$\rm ABCD$ et $\rm AEFG$ sont des carrés. Démontrer que
les droites $\rm (AI)$ et $\rm (ED)$ sont perpendiculaires. 		   
Corrigé en vidéo
Exercices 10:

Utiliser un produit scalaire pour savoir quand des droites sont perpendiculaires


$\rm ABCD$ est un rectangle. $\rm AB=5$ et $\rm AD=3$. $\rm E$ est un point de $\rm [DC]$.
Où placer le point $\rm E$ sur $\rm [DC]$ pour que les droites $\rm (AE)$ et $\rm (BD)$
soient perpendiculaires? 		   

Corrigé en vidéo
Exercices 11:

Droite perpendiculaire


Sur la figure ci-contre, $\rm ABCD$ est un carré.
$\rm E$ est un point de $\rm [AB]$ et $F$ un point de $\rm [AD]$ tel que $\rm AE = AF$.
$\rm G$ est le milieu de $\rm [DE]$.
Montrer que $(AG)$ et $(BF)$ sont perpendiculaires. 		   
Corrigé en vidéo
Exercices 12:

Calculer des longueurs à l'aide d'un produit scalaire


Dans le repère orthonormé ci-dessous, on a placé les points $\rm A$, $\rm B$ et $\rm C$.
$\rm H$ est le projeté orthogonal de $\rm C$ sur $\rm (AB)$.
Déterminer la valeur exacte de $\rm AH$. 		   
Corrigé en vidéo
Exercices 13:

Calculer des longueurs à l'aide d'un produit scalaire


On sait que $\rm AB=8$ m, $\rm BC=6$ m et $\rm AC=4$ m.
Déterminer la longueur $\rm AH$. 		   
Corrigé en vidéo
Exercices 14:

Calculer des longueurs à l'aide d'un produit scalaire


Benjamin doit calculer les longueurs des côtés du triangle $\rm ABC$ ci-dessous rectangle en $\rm A$.
$\rm H$ est le pied de la hauteur issue de $\rm A$.
Une tache d'encre l'en empêche. Comment peut-il faire? 		   
Corrigé en vidéo
Exercices 15:

Calculer des longueurs à l'aide d'un produit scalaire


$\rm ABC$ est un rectangle avec $\rm AB=6$ et $\rm AD=4$.
1. Montrer que $\rm \overrightarrow{AC}\cdot \overrightarrow{BD}=-20$.
2. En déduire que $\rm EF=\dfrac{10\sqrt {13}}{13}$. 		   
Corrigé en vidéo
Exercices 16:

Calculer un angle à l'aide du produit scalaire


Sur la figure ci-contre, $\mathrm{ABCD}$ est un carré.
$\mathrm{BCE}$ un triangle équilatéral de côté $1$.
1) Déterminer la mesure de l'angle $\widehat{\mathrm{ACE}}$ en radians.
2) On se place dans le repère orthonormé $(\rm A~;~\overrightarrow{\mathrm{AB}}~;~\overrightarrow{\mathrm{AD}})$.
    a) Déterminer les coordonnées du point $\rm E$.
    b) Calculer $\overrightarrow{\mathrm{CE}}.\overrightarrow{\mathrm{CA}}$.
3) En déduire que $\cos \dfrac{\pi}{12} = \dfrac{\sqrt{2} + \sqrt{6}}{4}$.
   
Corrigé en vidéo
Exercices 17:

Hauteur d'un triangle sont concourantes


Le but de cet exercice est de montrer que les hauteurs d'un triangle sont concourantes.
Soit $\rm ABC$ un triangle.
  1. Démontrer que pour tout point $M$ du plan, on a : $\overrightarrow{\rm AM}\cdot \overrightarrow{\rm BC} +\overrightarrow{\rm BM}\cdot \overrightarrow{\rm CA} + \overrightarrow{\rm CM}\cdot \overrightarrow{\rm AB} = 0$
  2. Soit $\rm H$ le point d'intersection des hauteurs du triangle $\rm ABC$ issues de $\rm A$ et $\rm B$.
    Démontrer à l'aide de l'égalité précédente que la troisième hauteur passe aussi par le point $\rm H$ et conclure.
Corrigé en vidéo
Exercices 18:

Inégalité de Cauchy-Schwarz


Soit $\vec u$ et $\vec v$ deux vecteurs.
1. Démontrer l'inégalité suivante appelée "Inégalité de Cauchy-Schwarz": $|\vec u \cdot \vec v|\leqslant ||\vec u||\times ||\vec v||$.
2. Démontrer qu'il y a égalité si et seulement si $\vec u$ et $\vec v$ sont colinéaires.