Limite infinie à l'infini
Définition :
Soit \(f\) une fonction définie sur un intervalle \(]a ;+\infty[\) (on dit que \(f\) est définie au voisinage de \(+\infty\)).
On dit que \(f\) a pour limite \(+\infty\) en \(+\infty\) si les images de \(x\) par la fonction \(f\) prennent des valeurs plus grandes que n'importe quel réel donné dès que \(x\) est assez grand.
Autrement dit, quel que soit le réel \(A\), il existe \(m>0\) tel que, pour tout \(x \in ]a ;+\infty[\), si \(x>m\), alors \(f(x)>A\).
On note alors \(\lim\limits_{x \to +\infty} f(x)=+\infty\).
Complément : à titre d'exercice...
On peut donner des définitions analogues d'une :
limite égale à \(-\infty\) en \(+\infty\)
limite égale à \(-\infty\) en \(-\infty\)
limite égale à \(+\infty\) en \(-\infty\)
Exemple : Limites usuelles
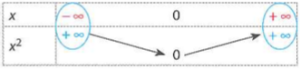
\(\lim\limits_{x \to +\infty} x^2=+\infty\)
\(\lim\limits_{x \to -\infty} x^2 = +\infty\)
\(\lim\limits_{x \to +\infty} \sqrt x=+\infty\)
Complément :
Pour démontrer ces résultats, inspirez-vous de l'activité précédente.
Remarque :
Si une fonction \(f\) admet une limite infinie en \(+\infty\), alors la suite de terme général \(u_n=f(n)\) a la même limite.
Attention :
La réciproque est fausse ! !
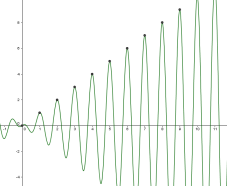
Exemple : \(f(x)=x\sin \left( \frac{\pi}{2}+2\pi x\right)\)
\(f(n)=n\) donc diverge vers \(+\infty\), mais \(f(x)\) oscille sans cesse et n'a pas de limite.
Méthode : Dresser un tableau de variation complet
Dorénavant, on fera figurer dans les tableaux de variations les limites éventuelles.
On lit sur ce tableau que \(\lim\limits_{x \to +\infty} x^2=+\infty\) et \(\lim\limits_{x \to -\infty} x^2=+\infty\)