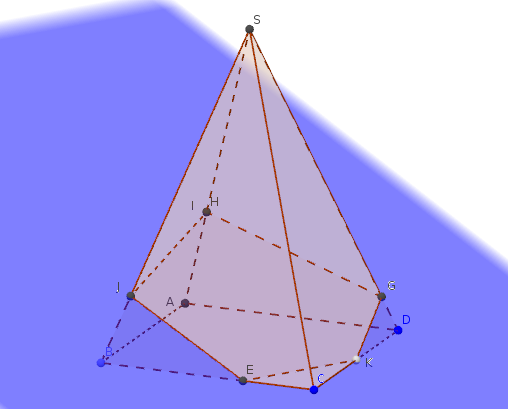
Exercice : Construire une section plane d'une pyramide

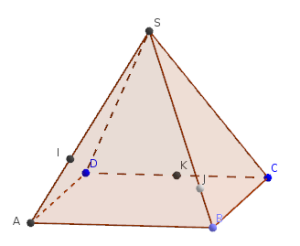
On considère une pyramide SABCD dont la base ABCD est un parallélogramme.

On définit :

  • les points I et J par \(\overrightarrow{SI}=\dfrac{2}{3}\overrightarrow{SA}~, ~~\overrightarrow{SJ}=\dfrac{4}{5}\overrightarrow{SB}\),

  • le point K milieu de [DC].

Question

Démontrer que la section de cette pyramide par le plan \(\mathcal P\) parallèle au plan (ABCD) et passant par I est un parallélogramme IEFG.

Indice

On se remémorera la partie du cours de seconde sur les plans parallèles.

Solution

D'après le second théorème sur les plans parallèles, on peut affirmer que :

  • Le plan (SAB) coupe les plans parallèles (ABCD) et \(\mathcal P\) suivant deux droites parallèles donc \((IE)//(AB)\).

  • De même avec le plan (SDC), \((FG)//(DC).\)

De plus, on sait que \((AB)//(DC)\) puisque ABCD est un parallélogramme.

On en conclut que \((IE)//(FG)\) et de manière analogue, \((EF)//(IG)\)

Ce qui démontre que IEFG est un parallélogramme.

Question

Déterminer la section de la pyramide avec le plan (IJK).

Indice

Solution

La droite (IJ) est incluse dans le plan (SAB). Elle coupe la droite (AB) en M qui est dans le plan (SAB) mais aussi dans le plan (ABCD).

Traçons la droite (KM). Celle-ci coupe (BC) en E.

  • M appartient à (IJK) (car M appartient à (IJ))

  • K appartient à (IJK)

Donc le point E construit appartient aussi à notre section de la pyramide par le plan (IJK).

Mais la droite (KM) coupe (AD) en N.

La droite (IN) est incluse :

  • dans le plan (IJK),

  • dans le plan (SAD).

Elle coupe la droite (SD) en G qui est donc le dernier point de notre section de la pyramide SABCD par (IJK).

Fianlement le plan (IJK) coupe la pyramide selon le polygone IJEKG.

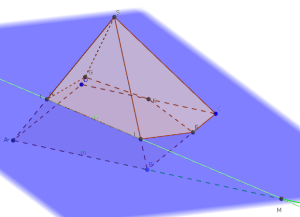
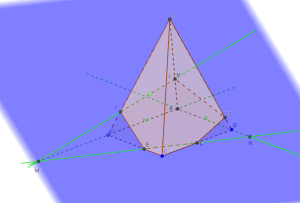
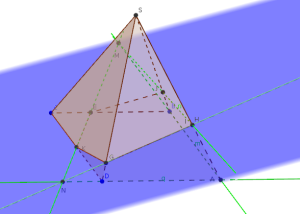
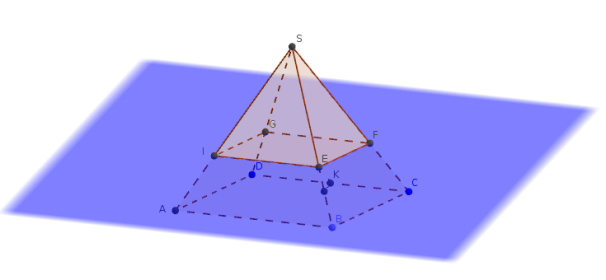
Autre vue :

Section d'une pyramide par un plan